Games101-Lecture 04 Transformation Cont

重点归纳:

1. 3D 变换(以旋转为重点):
   • 绕 x, y, z 轴旋转矩阵的差别, 循环对称性(列向量顺序问题)
   • 旋转的分解以及欧拉角, Rodrigues’ Rotation Formula(绕过原点的轴的旋转)
   • 四元数, 主要为了旋转间的差值(课程无), 因为旋转矩阵不太适合作差值, 三角函数不是线性的, (15 + 25)/2 != 20
2. Viewing 变换:
   • View(视图)/Camera 变换
   • 3D 到 2D 的投影变换(Orthographic/Perspective, 正交/透视)
3. View 变换
   • 标准相机位置的定义
   • 相机和模型的一起变换
4. 投影变换
   • 正交投影, 无近大远小
   • 简单的正交投影方法和常用的正交投影方法
   • 透视投影, 平行线会相交, 可以分解成”挤压”变换和正交投影变换
   • “挤压”变换的推导

一、3D 变换

1. 3D 缩放(Scale)

$$\large \mathbf{S}\left(s_{x}, s_{y}, s_{z}\right)=\left(\begin{array}{cccc}s_{x} & 0 & 0 & 0 \\ 0 & s_{y} & 0 & 0 \\ 0 & 0 & s_{z} & 0 \\ 0 & 0 & 0 & 1\end{array}\right)$$

2. 3D 平移(Translation)

$$\large \mathbf{T}\left(t_{x}, t_{y}, t_{z}\right)=\left(\begin{array}{cccc}1 & 0 & 0 & t_{x} \\0 & 1 & 0 & t_{y} \\0 & 0 & 1 & t_{z} \\0 & 0 & 0 & 1\end{array}\right)$$

3. 3D 旋转

绕坐标轴旋转

(1) 绕 x 轴旋转

$$\large \mathbf{R}_{x}(\alpha)=\left(\begin{array}{cccc}1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1\end{array}\right)$$

(2) 绕 y 轴旋转

$$\large \mathbf{R}_{y}(\alpha)=\left(\begin{array}{cccc}\cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1\end{array}\right)$$

(3) 绕 z 轴旋转

$$\large \mathbf{R}_{z}(\alpha)=\left(\begin{array}{cccc}\cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right)$$

Q: 只有绕 y 轴旋转时, 二维旋转矩阵是转置形式, 为什么?

A: 分析如下矩阵乘法, 其在形式上与上面的绕 y 轴旋转一致

$$\large \mathbf{R}_{-\alpha} \cdot \left[\begin{array}{l}x \\z\end{array}\right]=\left[\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha\end{array}\right] \cdot \left[\begin{array}{l}x \\z\end{array}\right]$$

而其几何含义是对于 xz 平面上的点, 将其沿 x 轴向 z 轴方向旋转$\large -\alpha$ 角度
即沿 z 轴向 x 轴方向旋转 $\large \alpha$角度, 也就是沿 y 轴旋转 $\large \alpha$ 角度;

反过来推导, 想要表达绕 y 轴旋转 $\large \alpha$ 角度, 就应该写成

$$\large \mathbf{R}_{\alpha} \cdot \left[\begin{array}{l}z \\x\end{array}\right]=\left[\begin{array}{cc}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha\end{array}\right] \cdot \left[\begin{array}{l}z \\x\end{array}\right]$$

那么写成和绕 x 、z 轴旋转一样的形式, 就相当于沿 x 轴向 z 轴方向旋转$\large -\alpha$ 角度, 也就是上面的样子;

以上体现了循环对称性, x -> yz, y->zx, z->xy , 可以看到只有 y -> zx 和列向量 $\large (x, y, z)^T$ 的顺序是反的, 所以旋转矩阵也是逆变换

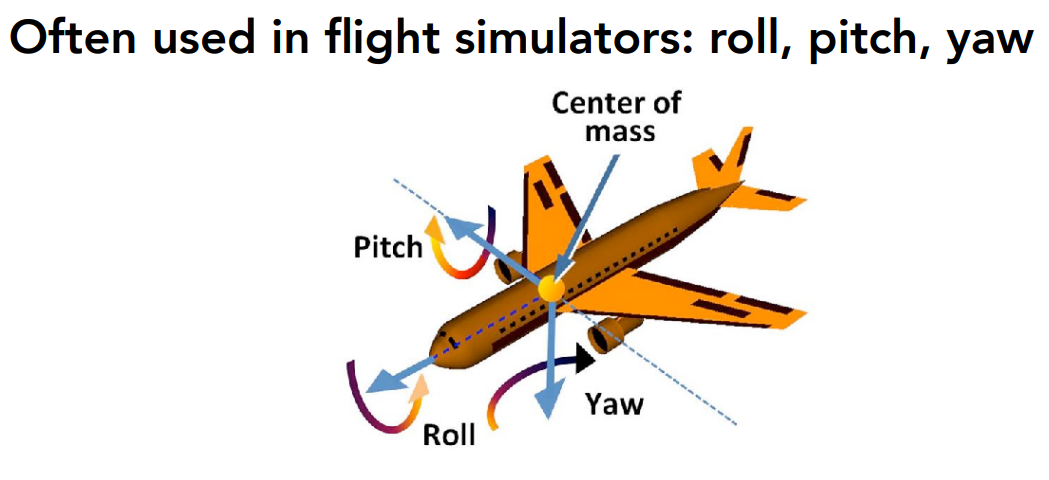
任意旋转都可以分解成绕 x 、y 、z 轴的旋转

$$\large R_{x y z}(\alpha, \beta, \gamma)=R_{x}(\alpha) R_{y}(\beta) R_{z}(\gamma)$$

• 四元数就是这种形式
• 本课程不会涉及四元数
• 四元数的旋转表示, 主要为了作旋转间的差值, 因为旋转矩阵不太适合作差值, 三角函数不是线性的, 15 度的旋转矩阵 + 25 度的旋转矩阵 / 2 != 20 度的旋转矩阵

绕过原点的任意轴旋转(Rodrigues’ Rotation Formula, $\large R(\vec{n},\alpha)$)

$$\large \mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^{T}+\sin (\alpha) \underbrace{\left(\begin{array}{ccc}0 & -n_{z} & n_{y} \\n_{z} & 0 & -n_{x} \\ -n_{y} & n_{x} & 0\end{array}\right)}_{\mathbf{N}}$$

为了表示任意的旋转, 可以:

平移到原点 -> 绕过原点的任意轴旋转 -> 平移回去

二、Viewing(观测)变换

老师将 Viewing 中文翻译成观测

分为两个步骤:

(1) View(视图)/Camera(相机)变换
(2) 3D 到 2D 的投影变换

Orthographic/Perspective Projection, 正交/透视投影

• MVP 变换: Model -> View -> Projection
• Model -> View 合称 ModelView Transformation, 因为 View 变换实际上是对相机和模型一起的变换
• View -> Projection 合称 Viewing 变换

1. 视图(View)/相机(Camera)变换

(1) 定义相机的位置 $\large \vec{e}$ 、朝向(Look-at/gaze) $\large \hat{g}$ 以及向上方向 $\large \hat{t}$

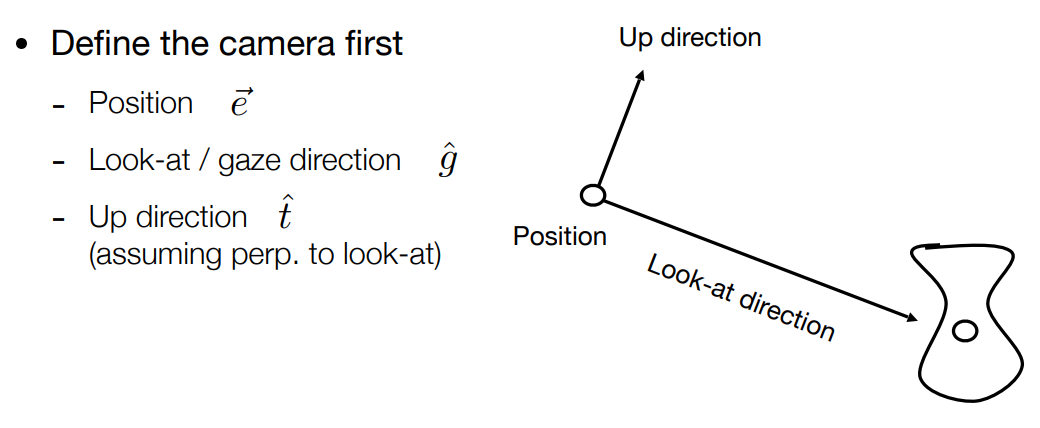
向上方向是为了确定相机的正倒

(2) 将相机和 Model 同时移动到标准位置, $\large M_{view}=R_{view}T_{view}$

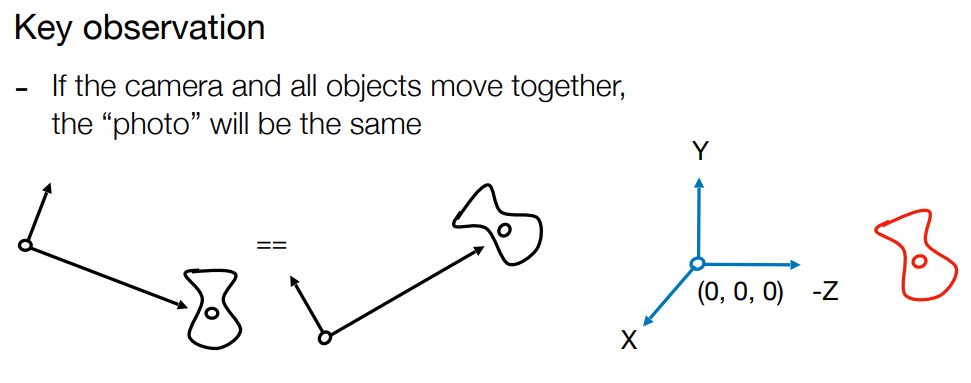
你动我也动相当于没动

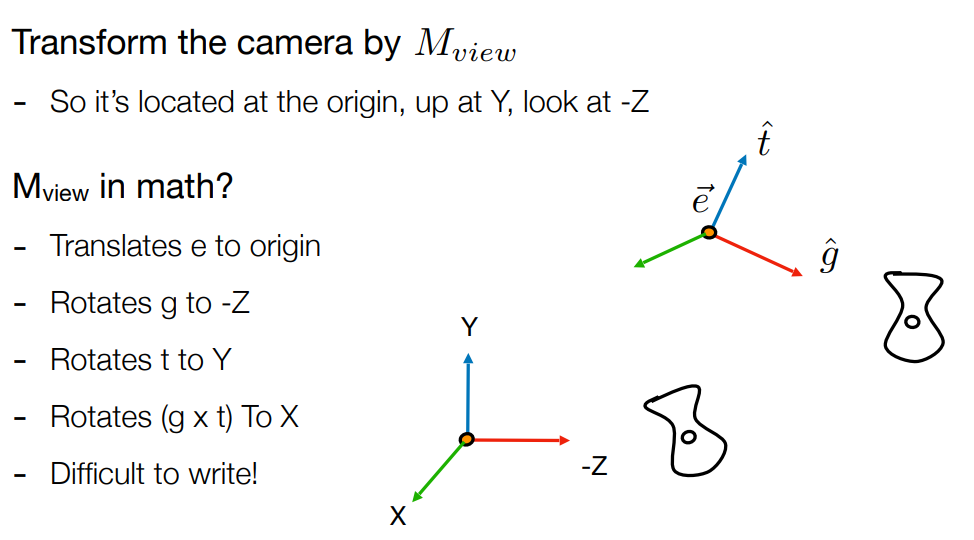
• 相机标准位置: up at Y , look at -Z

  这个标定位置是约定俗成的, OpenGL 用的也是这个位置

• 先平移到原定, $\large T_{view}$:

$$\large T_{\text {view }}=\left[\begin{array}{cccc}1 & 0 & 0 & -x_{e} \\0 & 1 & 0 & -y_{e} \\0 & 0 & 1 & -z_{e} \\0 & 0 & 0 & 1\end{array}\right]$$

• 再旋转, $\large R_{view}$:

$$\large R_{\text {view }}=\left[\begin{array}{cccc}x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\x_{t} & y_{t} & z_{t} & 0 \\x_{-g} & y_{-g} & z_{-g} & 0 \\0 & 0 & 0 & 1\end{array}\right]$$

$\large M_{view}$的推导:
旋转 $\large (\hat{g} \times \hat{t})$ to $\large \vec{X}$, $\large \hat{t}$ to $\large \vec{Y}$, $\large -\hat{g}$ to $\large \vec{Z}$
由于相机坐标系矩阵是一个正交矩阵, 所以其逆等于转置

2. 投影(Projection)变换

正交(Orthographic)投影

(1) 直接去掉 z 轴(实际上不用这种方法)

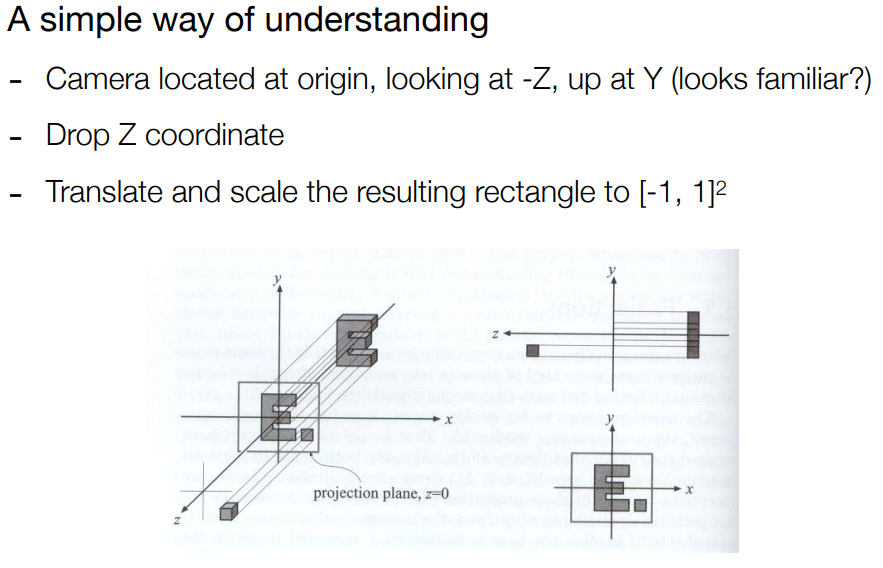
(2) 确定一个视野范围, 然后把该范围变换(标准化)为原点的一个 2 x 2 x 2 的立方体

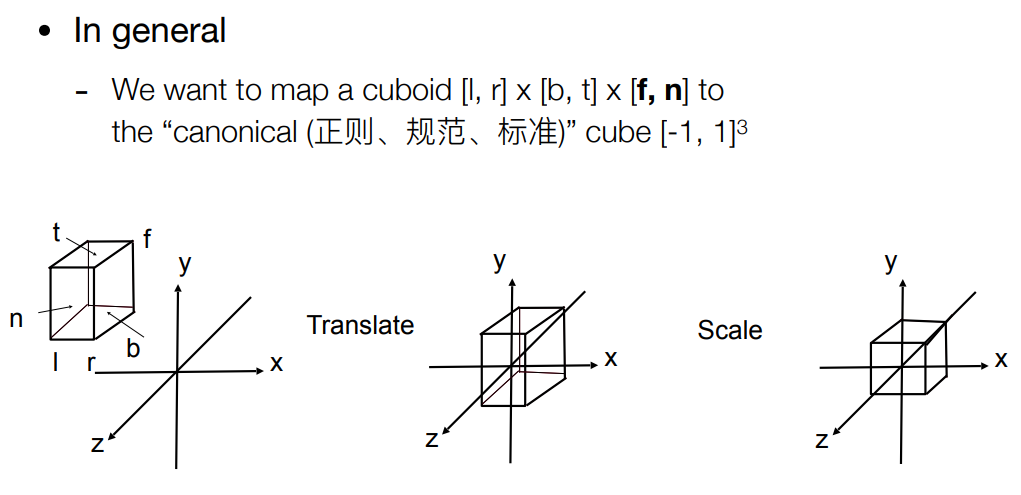
$$\large M_{\text {ortho }}=\left[\begin{array}{cccc}\frac{2}{r-l} & 0 & 0 & 0 \\0 & \frac{2}{t-b} & 0 & 0 \\0 & 0 & \frac{2}{n-f} & 0 \\0 & 0 & 0 & 1\end{array}\right]\left[\begin{array}{cccc}1 & 0 & 0 & -\frac{r+l}{2} \\0 & 1 & 0 & -\frac{t+b}{2} \\0 & 0 & 1 & -\frac{n+f}{2} \\0 & 0 & 0 & 1\end{array}\right]$$

• 先平移再缩放
• 正交投影变换的过程会使物体被拉伸,后面的还有视口变换

透视(Perspective)投影

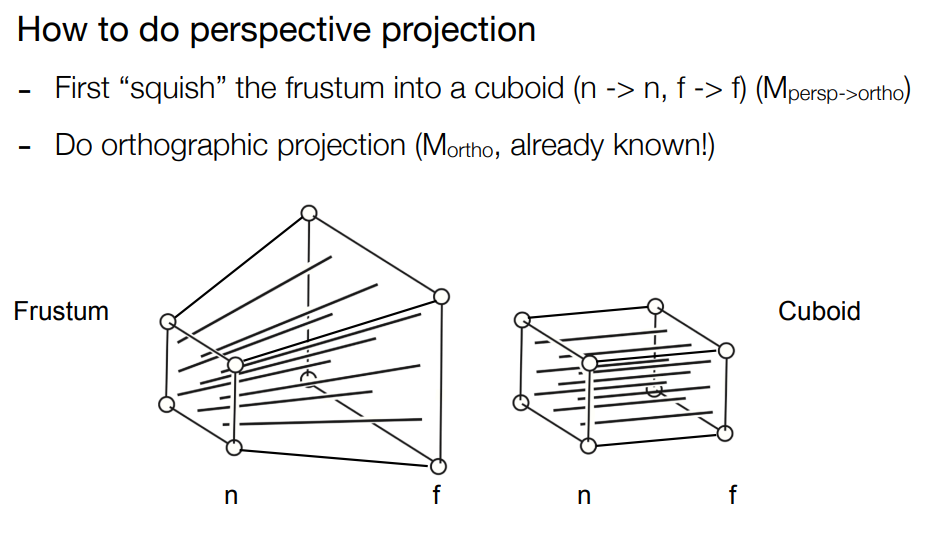
• 透视投影变换可以先把四棱台”挤压”成一个长方体, 再使用正交投影变换得到标准化的立方体
• 这个”挤压”操作要保证两点:
  • 近、远平面的 z 轴不会变
  • 远平面的中心不会变
  • 近平面的每个点都不变
• 注意四棱台上的点的 z 轴在”挤压”过程中是会变化的

这个”挤压”变换可以定义成 $\large M_{persp->ortho}$, 则投影变换为 $\large M_{persp}=M_{ortho}M{persp->ortho}$

重点就是推导这个”挤压”操作的变换矩阵,$\large M_{persp->ortho}$

推导:
$\large M_{persp->ortho} \cdot (x, y, z, 1)^T=(x^{\prime}, y^{\prime}, z^{\prime}, 1)^T$
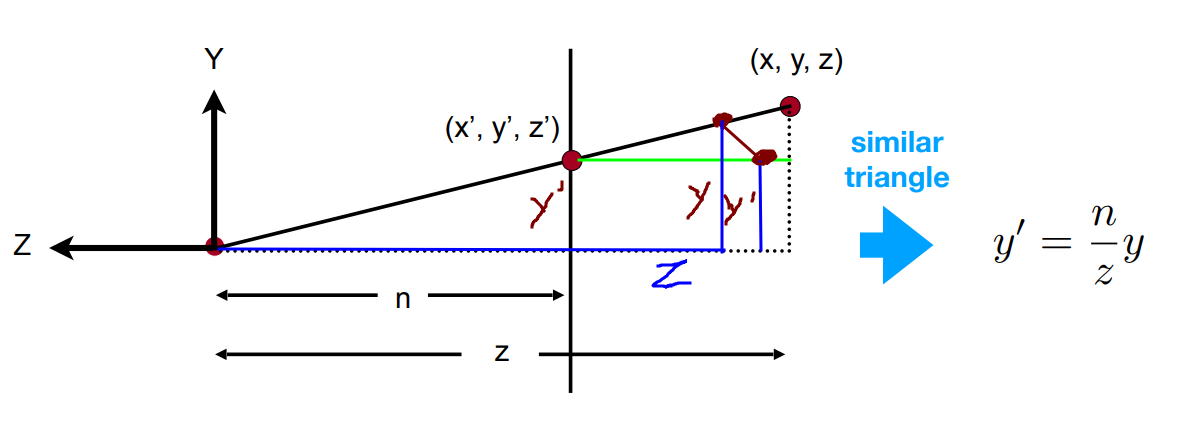
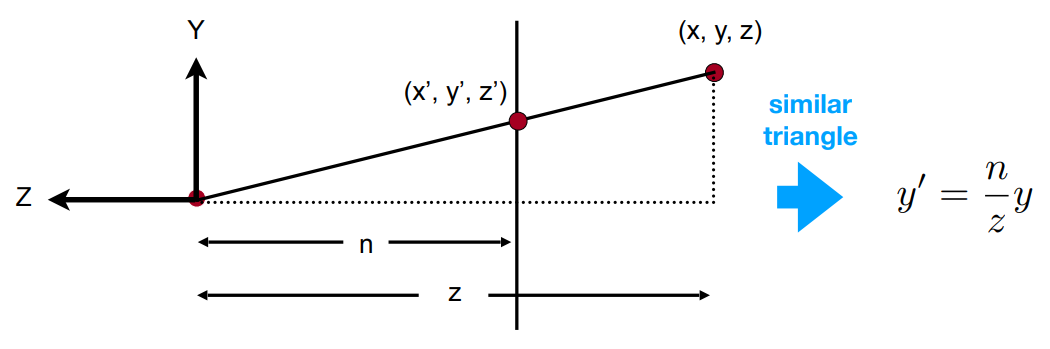
为了得到$\large M_{persp->ortho}$, 就需要知道 $\large x$ 与 $\large x^{\prime}$, $\large y$ 与 $\large y^{\prime}$ , $\large z$ 与 $\large z^{\prime}$的关系
前两者的关系根据相似三角形很容易得到(下图中手画的两个点, 上方的是”挤压”前的位置 $\large (x, y)$, 下方的是”挤压”后的位置 $\large (x^{\prime}, y^{\prime})$)

写成齐次坐标
$$\left(\begin{array}{l}x \\y \\z \\1\end{array}\right) \Rightarrow\left(\begin{array}{c}n x / z \\n y / z \\ \text{ unknown } \\1\end{array}\right)==\left(\begin{array}{c}n x \\n y \\ \text{ still unknown } \\z\end{array}\right)$$
然后可以推得
$$\large M_{\text {persp } \rightarrow \text { ortho }}=\left(\begin{array}{cccc}n & 0 & 0 & 0 \\0 & n & 0 & 0 \\ ? & ? & ? & ? \\0 & 0 & 1 & 0\end{array}\right)$$
利用远平面上中点不变, 和近平面上各点不变可得(后面我就直接放 ppt 的图了)
> >

Q :”挤压”操作究竟是让 z 变小还是变大

A : 答案是 z 会向 f 面靠近

上面推导了透视投影的”挤压”矩阵:

$$\large M_{\text {persp } \rightarrow \text { ortho }}=\left(\begin{array}{cccc}n & 0 & 0 & 0 \\0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\0 & 0 & 1 & 0\end{array}\right)$$

故有:

$$\large M_{\text {persp } \rightarrow \text { ortho }} \cdot \left(\begin{array}{l}x \\y \\z \\1\end{array}\right) =\left(\begin{array}{cccc}n & 0 & 0 & 0 \\0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\0 & 0 & 1 & 0\end{array}\right) \cdot \left(\begin{array}{l}x \\y \\z \\1\end{array}\right) = \left(\begin{array}{c}nx \\ ny \\ (n+f)z-nf \\ z \end{array}\right)$$

那么, 比较 $\large \frac{(n+f)z - nf}{z}$ 和 $\large z$ 的大小即可, 又因为
$$\large f \leq z \leq n < 0$$
若
$$\large z - \frac{(n+f)z - nf}{z} > 0 $$
则说明变换后 z 值更靠近 f 面, 离原点变远了, 上式变形得

$$\large \frac{z^2 - (n+f)z + nf}{z} > 0 $$

$$\large z^2 - (n+f)z + nf < 0 $$

$$\large (z-n)(z-f) < 0 $$

而 $\large (z-n)(z-f)$ 是小于等于 0 的, 所以挤压变换后 z 会靠近 f 面