Games101-Lecture 03 Transformation

重点归纳:

1. 2D 变换:
   • 线性变换(Linear):缩放(scale)、切变(shear)、旋转(rotatrion)、镜像(Reflection)
   • 非线性变换:平移(translation)
   • 仿射变换(Affine): 线性变换 + 平移
2. 齐次坐标
   • 用线性矩阵来描述上述所有的变换
   • 点与向量的表示
3. 变换的组合与分解
   • 变换的先后顺序
   • 绕任意点的旋转

一、2D 变换(Transformation)

变换的分类:

• 模型变换(Modeling):
  • 2D 变换
  • 3D 变换
• 观测变换(Viewing):
  • View(视图)/Camera 变换
  • 3D 到 2D 的投影变换(Orthographic/Perspective, 正交/透视)

1. 缩放(scale)

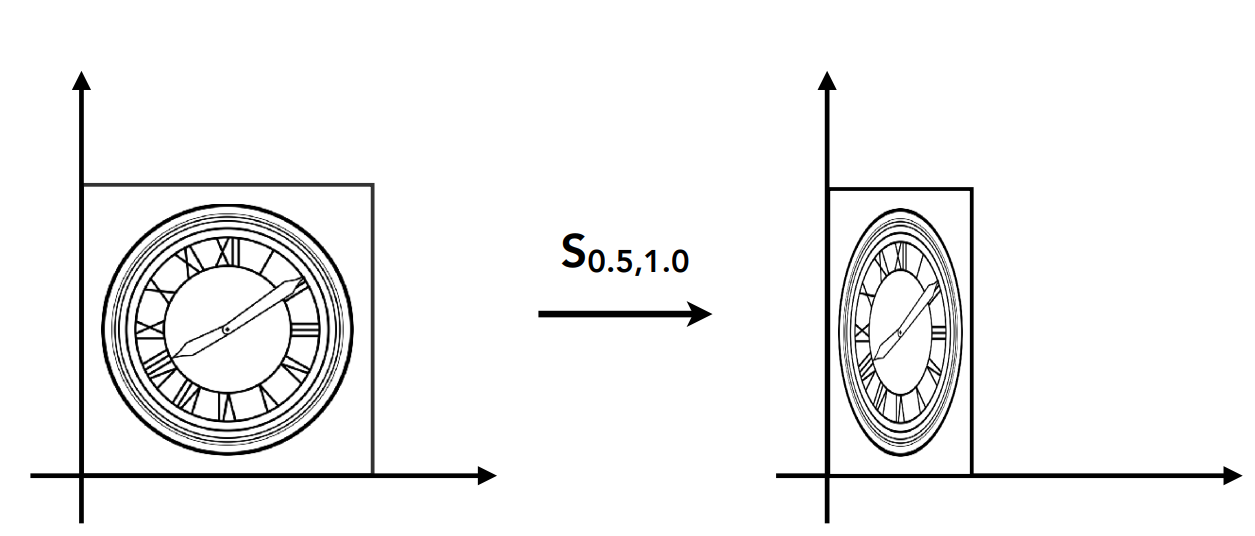
$$\large \left[\begin{array}{l}x^{\prime} \\y^{\prime}\end{array}\right]=\left[\begin{array}{ll}0.5 & 0 \\0 & 1\end{array}\right]\left[\begin{array}{l}x \\y\end{array}\right]$$

2. 镜像(Reflection)

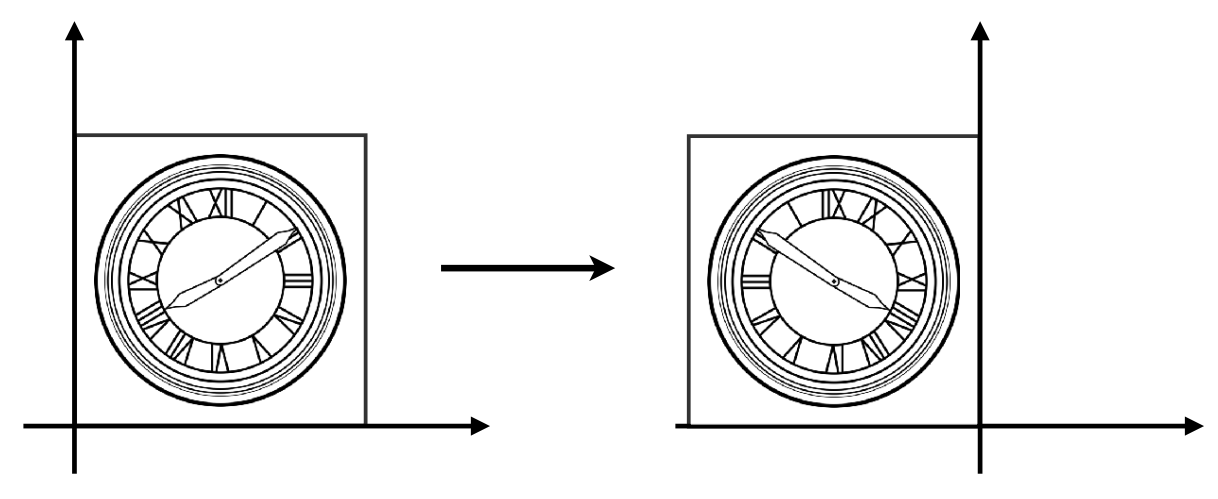
$$\large \left[\begin{array}{l}x^{\prime} \\y^{\prime}\end{array}\right]=\left[\begin{array}{ll}-1 & 0 \\0 & 1\end{array}\right]\left[\begin{array}{l}x \\y\end{array}\right]$$

3. 切变(shear)

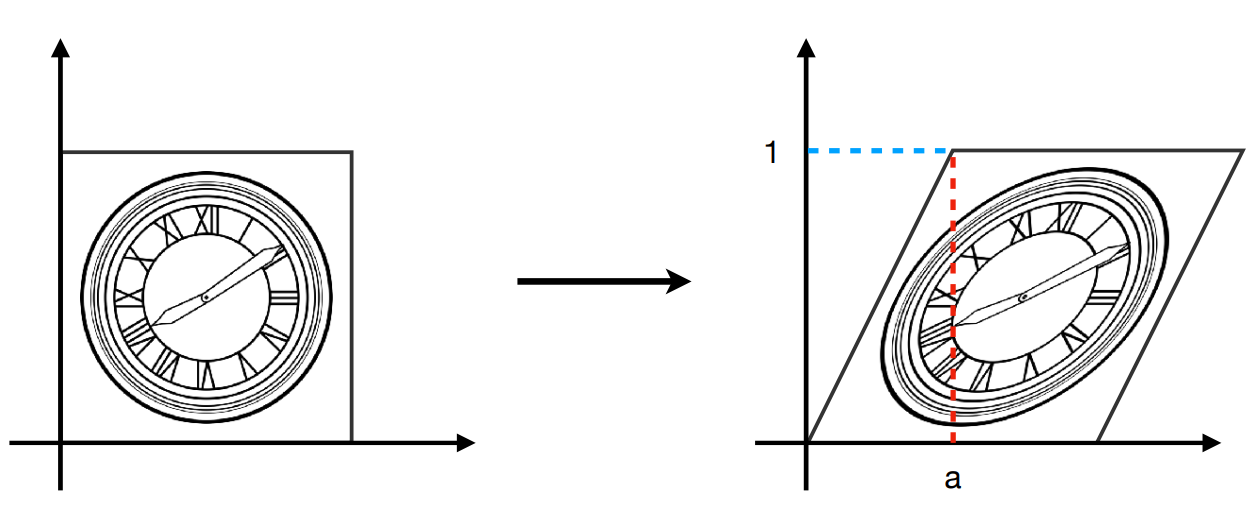
$$\large \left[\begin{array}{l}x^{\prime} \\y^{\prime}\end{array}\right]=\left[\begin{array}{ll}1 & a \\0 & 1\end{array}\right]\left[\begin{array}{l}x \\y\end{array}\right]$$

$$\large \begin{array}{l}x^{\prime}=x+a y \\y^{\prime}= y\end{array}$$

• 通过特殊点(0,1)->(a,1)推导而来

4. 旋转(rotate)

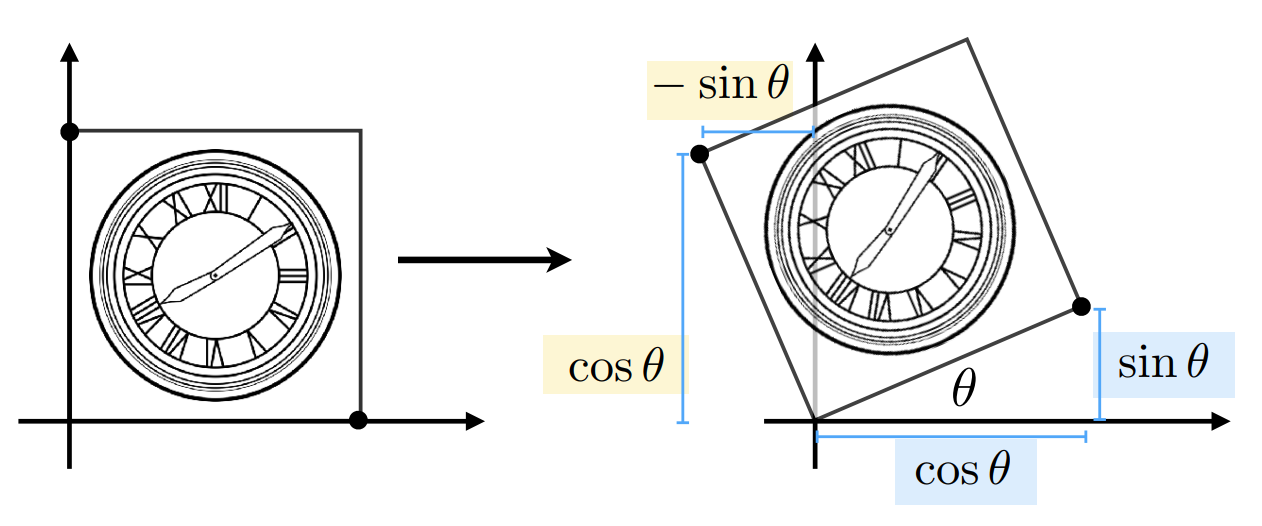
$$\large \mathbf{R}_{\theta}=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\sin \theta & \cos \theta\end{array}\right]$$

• 考虑正方形的边长为 1 的特殊情况, 可简单推得

同时旋转矩阵也是一个正交矩阵, 因为其逆变换为旋转$\large -\theta$, 也就是说其逆变换矩阵为:

$$\large \mathbf{R}_{-\theta}=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\end{array}\right]$$

而该矩阵刚好是 $\large \mathbf{R}_{\theta}$ 的转置

逆变换矩阵 = 变换矩阵的逆
正交矩阵即左乘其转置等于单位矩阵的矩阵
正交矩阵的逆等于其转置
正交矩阵的列向量为两两垂直的单位向量

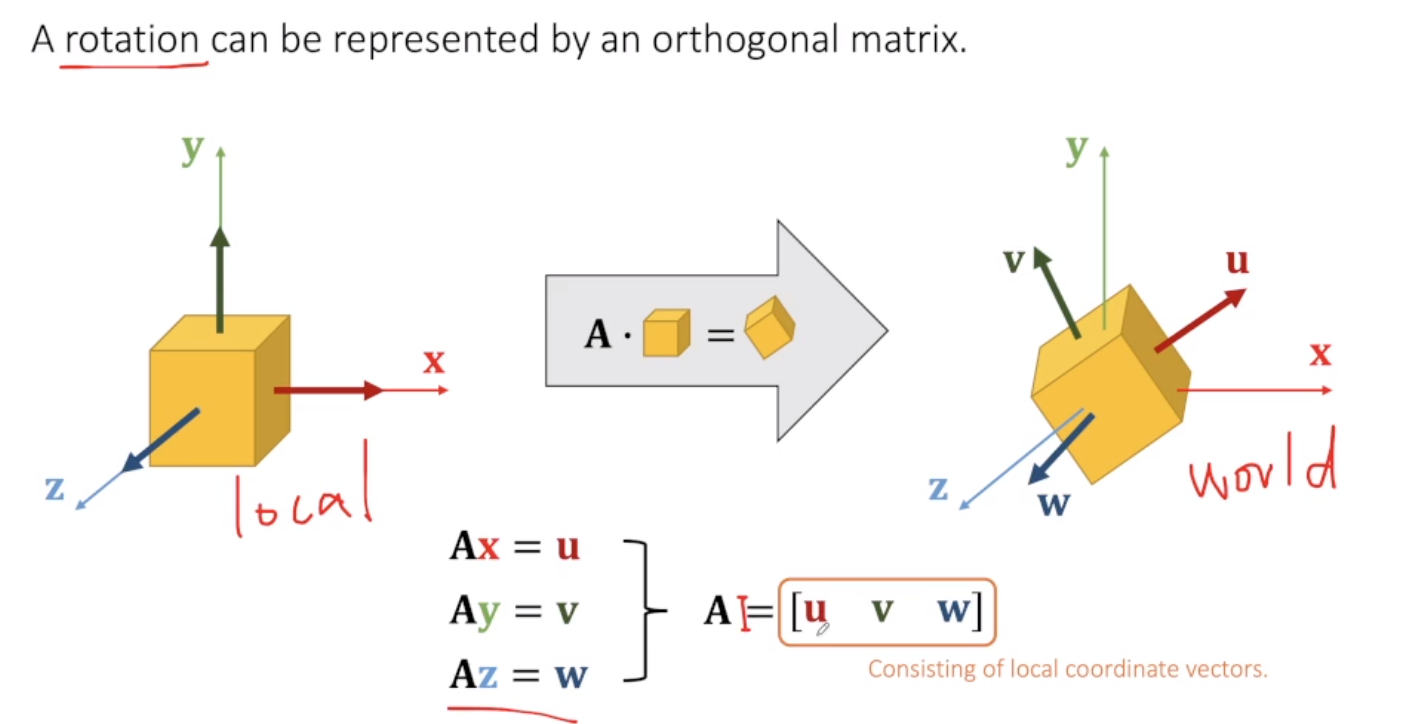
关于旋转矩阵是正交矩阵, Games103 中也有一种解释, 即旋转操作相当于对坐标系的旋转

线性变换的矩阵形式

$$\large \begin{array}{l}x^{\prime}=a x+b y \\y^{\prime}=c x+d y\end{array}$$

$$\large \left[\begin{array}{l}x^{\prime} \\y^{\prime}\end{array}\right]=\left[\begin{array}{ll}a & b \\c & d\end{array}\right]\left[\begin{array}{l}x \\y\end{array}\right]$$

$$\large \mathbf{x}^{\prime}=\mathbf{M} \mathbf{x}$$

5. 平移(translation)

$$\large \begin{array}{l}x^{\prime}=x+t_{x} \\y^{\prime}=y+t_{y}\end{array}$$

平移变换虽然形式简单, 但无法写成矩阵的线性变换

$$\large \left[\begin{array}{l}x^{\prime} \\y^{\prime}\end{array}\right]=\left[\begin{array}{ll}a & b \\c & d\end{array}\right]\left[\begin{array}{l}x \\y\end{array}\right]+\left[\begin{array}{l}t_{x} \\t_{y}\end{array}\right]$$

二、齐次坐标(Homogenous Coordinates)

1. 使用齐次坐标的目的

为了将以上的变换的矩阵形式统一起来而发明

• 2D Point = $\large (x, y, 1)^{\top}$
• 2D Vector = $\large (x, y, 0)^{\top}$

trade off/no free lunch:

• 优点: 统一了仿射变换的矩阵形式
• 缺点: 需要多一维的空间

同时也保证了运算的合理性

• vector + vector = vector
• point - point = vector
• point + vector = point
• point + point = ??

$$\large \left(\begin{array}{c}x \\y \\w\end{array}\right) \text { is the } 2 \mathrm{D} \text { point }\left(\begin{array}{c}x / w \\y / w \\1\end{array}\right), w \neq 0$$

可以推得, 两个点相加得到的是他们的中点

2. 齐次坐标下, 仿射变换矩阵的特点

Scale

$$\large \mathbf{S}\left(s_{x}, s_{y}\right)=\left(\begin{array}{ccc}s_{x} & 0 & 0 \\0 & s_{y} & 0 \\0 & 0 & 1\end{array}\right)$$

Rotation

$$\large \mathbf{R}(\alpha)=\left(\begin{array}{ccc}\cos \alpha & -\sin \alpha & 0 \\sin \alpha & \cos \alpha & 0 \\0 & 0 & 1\end{array}\right)$$

Translation

$$\large \mathbf{T}\left(t_{x}, t_{y}\right)=\left(\begin{array}{ccc}1 & 0 & t_{x} \\0 & 1 & t_{y} \\0 & 0 & 1\end{array}\right)$$

三、变换的组合(Composing Transforms)

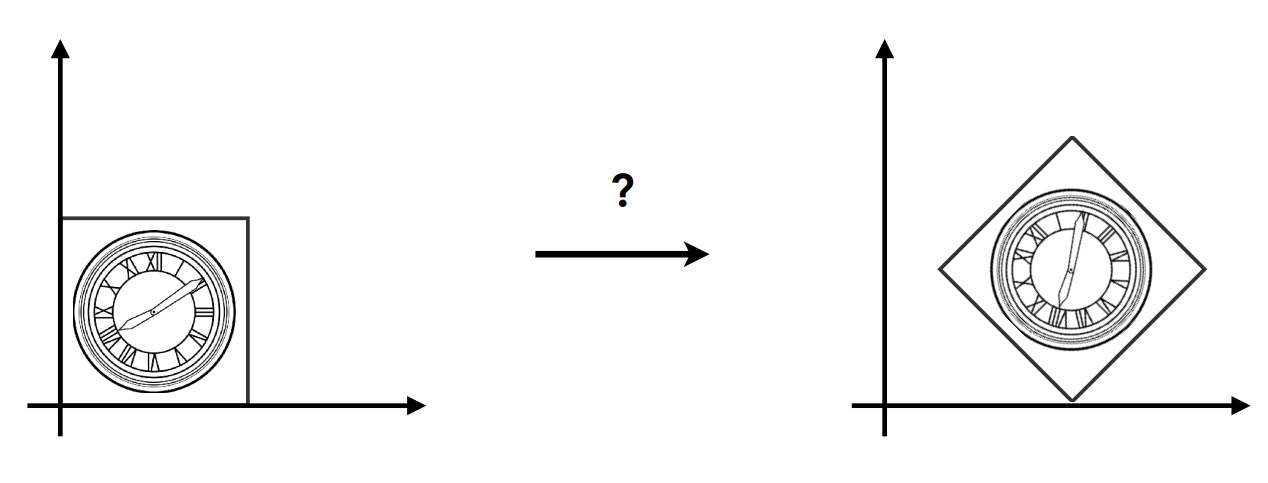
复杂变换可以通过简单变换得到

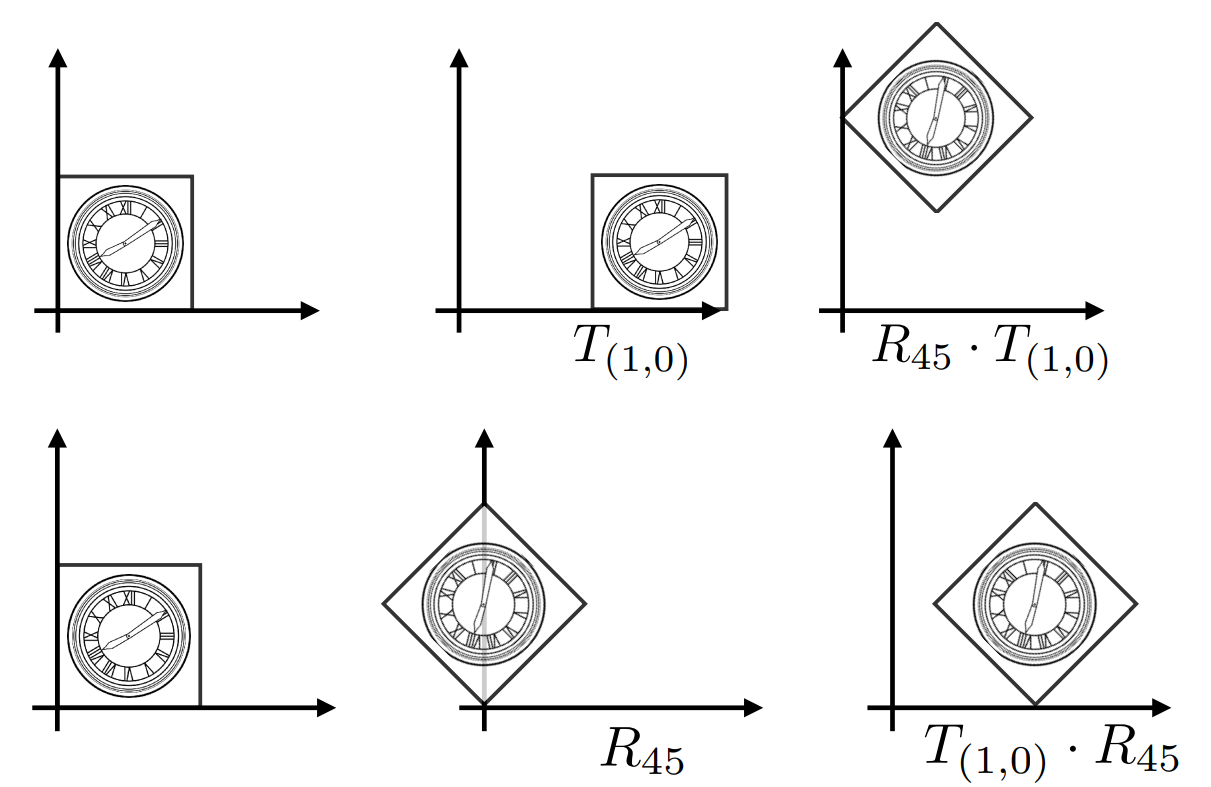
顺序很重要, 先旋转再平移

$$\large T_{(1,0)} \cdot R_{45}\left[\begin{array}{l}x \\y \\1\end{array}\right]=\left[\begin{array}{lll}1 & 0 & 1 \\0 & 1 & 0 \\0 & 0 & 1\end{array}\right]\left[\begin{array}{ccc}\cos 45^{\circ} & -\sin 45^{\circ} & 0 \\sin 45^{\circ} & \cos 45^{\circ} & 0 \\0 & 0 & 1\end{array}\right]\left[\begin{array}{l}x \\y \\1\end{array}\right]$$

矩阵乘法满足结合律, 变换的顺序是从右到左, 但计算的顺序可以从左到右

Q: 以任意点为中心旋转?

A: 变换的分解, 先平移到中心, 再旋转, 再平移回去

$$\large \mathbf{T}(\mathbf{c}) \cdot \mathbf{R}(\alpha) \cdot \mathbf{T}(-\mathbf{c})$$

四、3D 变换(3D Transforms)

• 3D Point = $\large (x, y, z, 1)^{\top}$
• 3D Vector = $\large (x, y, z, 0)^{\top}$

对于第四维为 w 的点:

$$\large (x, y, z, w) = (x / w, y / w, z / w, 1)$$

$$\large \left(\begin{array}{l}x^{\prime} \\y^{\prime} \\z^{\prime} \\1\end{array}\right)=\left(\begin{array}{lllc}a & b & c & t_{x} \\d & e & f & t_{y} \\g & h & i & t_{z} \\0 & 0 & 0 & 1\end{array}\right) \cdot\left(\begin{array}{l}x \\y \\z \\1\end{array}\right)$$

Q: 齐次坐标下 4x4 的仿射变换矩阵是先线性变换? 还是先平移
A: 相当于普通坐标下先线性变换再平移