Games101：Lecture 02 Review of Linear Algebra

Games101 Lecture 01 是一些图形学的基本介绍, 我就不记录了, 从 Lecture 02 开始

重点归纳:

1. 向量点乘可以用于计算向量间的余弦夹角, 从而得知向量互相的接近程度
2. 向量点乘可以用于计算向量的投影, 可以用于向量的分解, 将向量分解成两个垂直的向量
3. 向量点乘可以用于计算向量的方向性, 判断两个向量是同向还是异向, 以及它们的接近程度
4. 向量叉乘的结果是一个向量, 由右手螺旋定则决定方向
5. 向量叉乘可以用于判断向量的左右关系, 判断点在三角形的内部还是外部
6. 矩阵在图形学中的应用: 变换

阅读材料：Fundamentals of Computer Graphics（3rd or 4th ）, 第二章 （Miscellaneous Math）、第五章（Linear Algebra）

A Swift and Brutal Introduction to Linear Algebra!

一、向量(Vectors)

1. 向量的构成与特点

$${\large \overrightarrow{a}=\overrightarrow{A B}=B-A}$$

• 向量通常写作${\large \overrightarrow{a}}$或者${\large \mathbf{a}}$
• A 指向 B 的向量 = B 的坐标减去 A 的坐标
• 向量具有长度和方向两个属性
• 向量只要长度和方向相同就是相等的, 并不关心其起始位置

2. 向量标准化(Vector Normalization)

$${\large \hat{a}=\vec{a} /|\vec{a}|}$$

• 向量的长度被写作${\large |\vec{a}|}$
• 单位向量(Unit Vector)就是长度为 1 的向量
• 单位向量用于表示方向而不关心其长度

3. 向量求和(Vextor Addition)

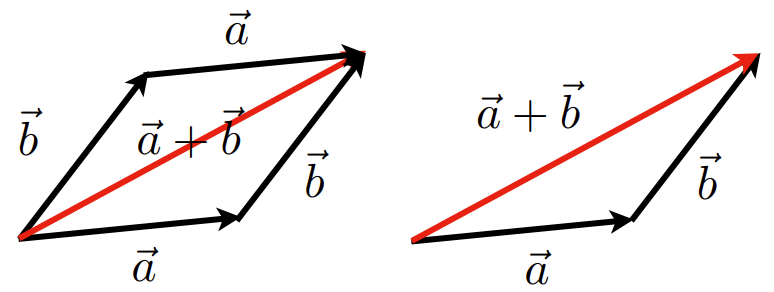
• 几何：平行四边形法则和三角形法则
• 代数：坐标相加

4. 向量的坐标表示(Cartesian Coordinates)

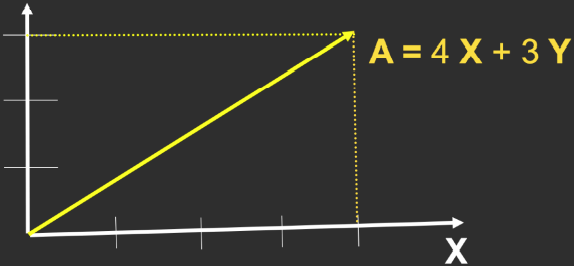
• ${\large \mathbf{X}}$、${\large \mathbf{Y}}$是正交（垂直在高维空间中的推广）的单位向量, 分别是笛卡尔坐标系横轴和纵轴的方向
• 图形学上默认向量是列向量的形式:${\large \mathbf{A}=\left(\begin{array}{l}x \\y\end{array}\right)=\left(\begin{array}{l}4 \\3\end{array}\right)}$

5. 向量的点乘(Vector Dot Product)

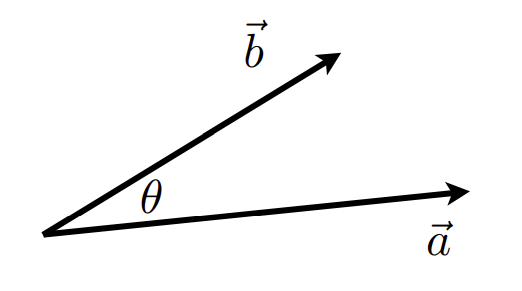
$${\large \vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta}$$
$${\large \cos \theta=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}}$$
$${\large \cos \theta=\hat{a} \cdot \hat{b}}$$

• 向量的点乘结果是一个值
• 已知两个向量的坐标表示, 可以求他们之间的夹角, 余弦夹角
• 两个单位向量的夹角就是他们的点乘

5.1 向量点乘的性质

$${\large \vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}}$$
$${\large \vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}}$$
$${\large (k \vec{a}) \cdot \vec{b}=\vec{a} \cdot(k \vec{b})=k(\vec{a} \cdot \vec{b})}$$

• 当三个向量进行点乘时, 后两个向量是不满足交换率和结合率的

5.2 在笛卡尔坐标系下的点乘计算

$${\large \vec{a} \cdot \vec{b}=\left(\begin{array}{l}x_{a} \\y_{a}\end{array}\right) \cdot\left(\begin{array}{l}x_{b} \\y_{b}\end{array}\right)=x_{a} x_{b}+y_{a} y_{b}}$$

$${\large \vec{a} \cdot \vec{b}=\left(\begin{array}{l}x_{a} \\y_{a} \\z_{a}\end{array}\right) \cdot\left(\begin{array}{l}x_{b} \\y_{b} \\z_{b}\end{array}\right)=x_{a} x_{b}+y_{a} y_{b}+z_{a} z_{b}{\Huge }}$$

5.3 利用点乘求解投影(Dot Product for Projection)

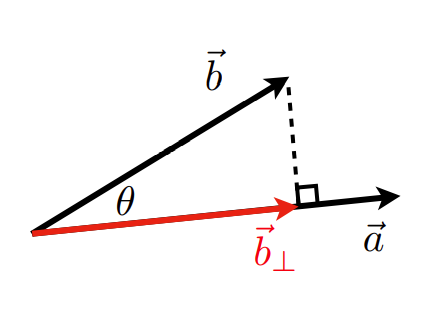
$${\large \vec{b}_{\perp}=k \hat{a}}$$

$${\large k=\left|\vec{b}_{\perp}\right|=|\vec{b}| \cos \theta} $$

$${\large \vec{b}_{\perp}=|\vec{b}| \cos \theta \hat{a}=|\vec{b}| \hat{a} \hat{b} \hat{a}=\vec{b} \hat{a} \hat{a}}$$

• 向量的投影可以用于分解向量, 将$\large \vec{b}$分解成两个互相垂直的向量 $\large \vec{b}_{\perp}$ 和 $\large \vec{b}-\vec{b}_{\perp}$

5.4 利用点乘判断向量间的方向(Dot Product in Graphics)

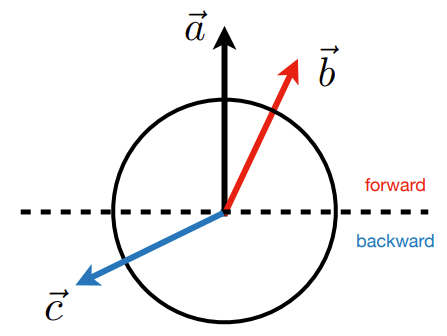
• 求解$\large \vec{a}$和$\large \vec{c}$、$\large \vec{b}$的余弦夹角
• 若$\large \cos \theta > 0$,则与$\large \vec{a}$同向
• 若$\large \cos \theta = 0$,则与$\large \vec{a}$垂直
• 若$\large \cos \theta < 0$,则与$\large \vec{a}$异向
• 若$\large \cos \theta$越接近$1$,则越接近$\large \vec{a}$

应用: 金属的高光, 镜面反射, 用于判断出射光和相机法向的接近关系

6. 向量的叉乘(Cross Product)

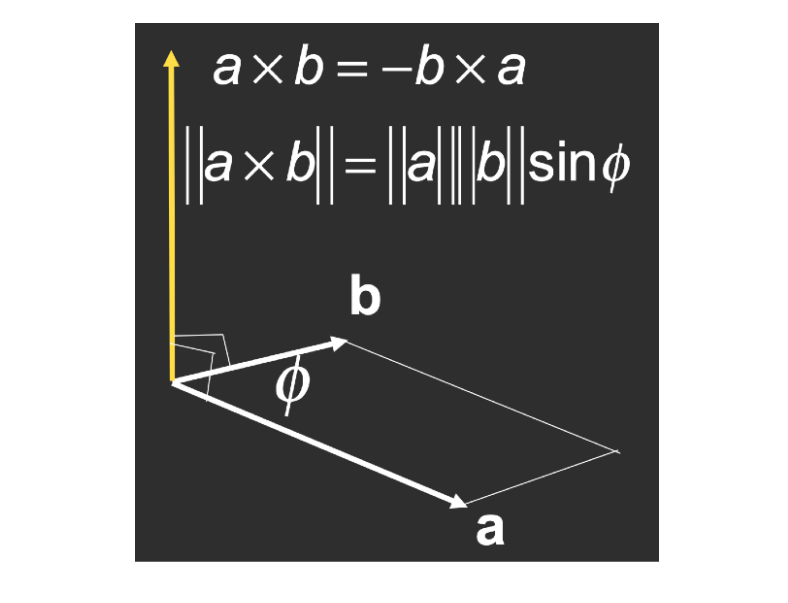
叉乘的结果是一个向量

• 右手螺旋定则确定叉乘的方向
• 向量的大小为 $\large |\vec{a}| * |\vec{b}| * \sin \theta$

应用:

• 构造坐标系
• 判断坐标系的左右手: $\large \vec{x} \times \vec{y}$ 得到 $\large \vec{z}$ , 则说明坐标系的方向是右手坐标系, 得到 $\large -\vec{z}$ 则是左手坐标系

6.1 向量叉乘的计算(Cross Product: Cartesian Formula)

$$\large \vec{a} \times \vec{b} = \left(\begin{array}{c} y_{a} z_{b}-y_{b} z_{a} \\ z_{a} x_{b}-x_{a} z_{b} \\ x_{a} y_{b}-y_{a} x_{b} \end{array}\right)$$

$$\large \vec{a} \times \vec{b}=A^{*} b=\left(\begin{array}{ccc} 0 & -z_{a} & y_{a} \\ z_{a} & 0 & -x_{a} \\ -y_{a} & x_{a} & 0 \end{array}\right)\left(\begin{array}{l} x_{b} \\ y_{b} \\ z_{b} \end{array}\right)$$

• A 是一个对偶矩阵

6.2 向量叉乘的性质(Cross product: Properties)

$$\large \begin{array}{lc} \vec{x} \times \vec{y}=+\vec{z} & \vec{a} \times \vec{b}=-\vec{b} \times \vec{a} \\ \vec{y} \times \vec{x}=-\vec{z} & \vec{a} \times \vec{a}=\overrightarrow{0} \\ \vec{y} \times \vec{z}=+\vec{x} & \vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c} \\ \vec{z} \times \vec{y}=-\vec{x} & \vec{a} \times(k \vec{b})=k(\vec{a} \times \vec{b}) \\ \vec{z} \times \vec{x}=+\vec{y} & \\ \vec{x} \times \vec{z}=-\vec{y} & \end{array}$$

6.3 向量叉乘的应用

判断向量的左右关系:

• 如图, $\large \vec{a} \times \vec{b}$, 其 z 坐标大于 0, $\large \vec{a}$ 在 $\large \vec{b}$ 的右侧
• 如图, $\large \vec{a} \times \vec{b}$, 其 z 坐标小于 0, $\large \vec{a}$ 在 $\large \vec{b}$ 的左侧

判断点在三角形的内部还是外部:

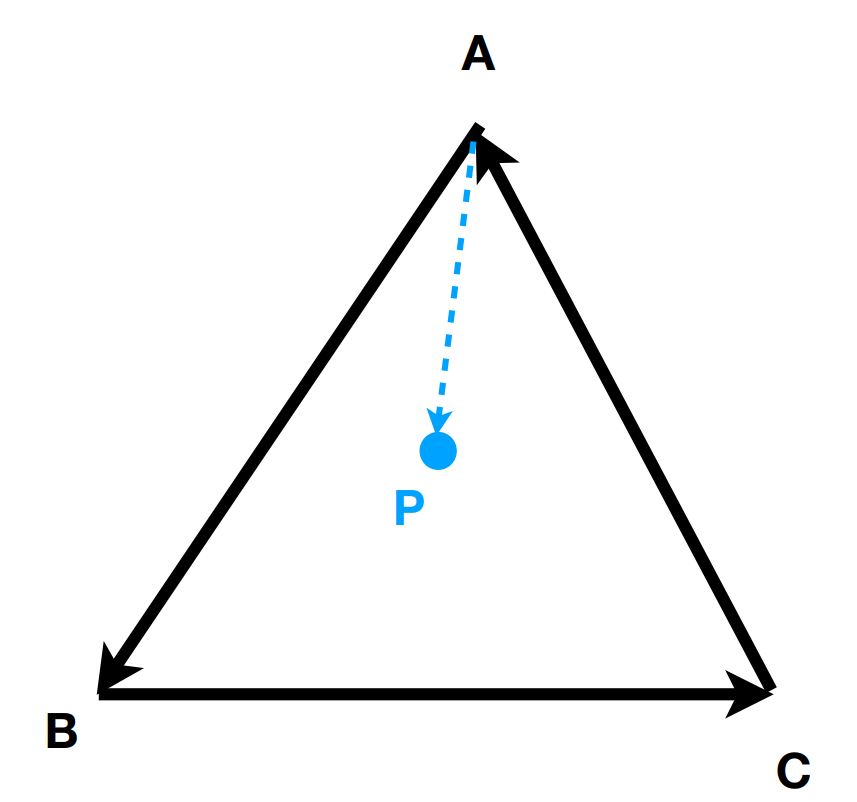
• $\large \vec{AB} \times \vec{AP}$, 结果向外, P 在 AB 的左侧
• $\large \vec{BC} \times \vec{BP}$, 结果向外, P 在 BC 的左侧
• $\large \vec{CA} \times \vec{CP}$, 结果向外, P 在 CA 的左侧
• 则说明 P 在三角形 ABC 内部

对于三角形 CBA, 则 P 一定都在其右侧, 如果刚好 P 点在与某一个向量的叉乘为 0, 与其他两个向量的叉乘为同侧, 则说明 P 在三角形上, 这种情况自己定义是在内部还是在外部

二、正交基与坐标系(Orthonormal bases and coordinate frames)

1. 自定义坐标系

$$\large \begin{array}{l} n|\vec{u}|=|\vec{v}|=|\vec{w}|=1 \\ \vec{u} \cdot \vec{v}=\vec{v} \cdot \vec{w}=\vec{u} \cdot \vec{w}=0 \\ \vec{w}=\vec{u} \times \vec{v} \quad \text { (right-handed) } \end{array}$$

• $\large \hat{u}$, $\large \hat{v}$, $\large \hat{w}$ 为互相垂直的单位向量

$$\large \begin{array}{l} \vec{p}=(\vec{p} \cdot \vec{u}) \vec{u}+(\vec{p} \cdot \vec{v}) \vec{v}+(\vec{p} \cdot \vec{w}) \vec{w}\\ \text { (projection) } \end{array}$$

• 向量$\large \vec{p}$通过投影分解

三、矩阵(Matrices)

主要应用于矩阵变换(Transformations)

• Translation, Rotation, Shear, Scale

1. 矩阵乘法(Matrix-Matrix Multiplication)

$$\large \left(\begin{array}{ll} 1 & 3 \\ 5 & 2 \\ 0 & 4 \end{array}\right)\left(\begin{array}{llll} 3 & 6 & 9 & 4 \\ 2 & 7 & 8 & 3 \end{array}\right)$$

• 需要满足要求: (M x N) (N x P) = (M x P)

$$\large \left(\begin{array}{ll} 1 & 3 \\ 5 & 2 \\ 0 & 4 \end{array}\right)\left(\begin{array}{llll} 3 & 6 & 9 & 4 \\ 2 & 7 & 8 & 3 \end{array}\right)=\left(\begin{array}{cccc} 9 & ? & 33 & 13 \\ 19 & 44 & 61 & 26 \\ 8 & 28 & 32 & ? \end{array}\right)$$

• Element (i, j) in the product is the dot product of row i from A and column j from B

2. 矩阵乘法的运算律/性质(Properties)

$${\large (AB)C=A(BC)}$$
$${\large A(B+C) = AB + AC}$$
$${\large (A+B)C = AC + BC}$$

• 不满足交换律
• 满足结合律和分配律

3. 矩阵与列向量

• 在图形学中, 向量用列向量表示是为了方便左乘一个矩阵
• 向量的点乘和叉乘都可以写成矩阵乘法

4. 矩阵的转置

$$\large \left(\begin{array}{ll}1 & 2 \\3 & 4 \\5 & 6\end{array}\right)^{T}=\left(\begin{array}{lll}1 & 3 & 5 \\2 & 4 & 6\end{array}\right)$$

$$\large (A B)^{T}=B^{T} A^{T}$$

• 矩阵转置的运算性质

5. 单位矩阵与矩阵的逆

$$\large \begin{array}{l}I_{3 \times 3}=\left(\begin{array}{ccc}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1\end{array}\right) \\A A^{-1}=A^{-1} A=I \(A B)^{-1}=B^{-1} A^{-1}\end{array}$$